Most people know the Pythagorean theorem:
a2 + b2 = c2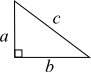
The longest side is always c. It is called the hypotenuse. The sum of the squares of the other two sides (a and b) always equals the square of the hypotenuse. You can say that a bajillion different ways, but it always means this beautiful little equation: a2 + b2 = c2.
The 3-4-5 Right Triangle:
If you plug in 3 for a and 4 for b, you will always, always, ALWAYS get 5.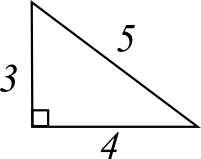
32 + 42 = c2
9 + 16 = c2
25 = c2
√ 25 = √ c 2
5 = c
The sequence 3-4-5 is called a “Pythagorean triple.” It holds true for all the multiples of 3-4-5. For example, multiplying each side by 2 will give you 6 and 8 for the shorter sides, and the hypotenuse will always be 10. So, 3-4-5 is a triple, and so is 6-8-10. So is 9-12-15 and so on to infinity.
Standardized tests frequently use triples in their questions, so you gain an advantage by memorizing some of the most common ones below:
3-4-5 (and multiples)
5-12-13 ( and multiples)
7-24-25 (and multiples)
11-60-61 (and multiples)
The Isosceles Right Triangle:
Standardized tests also love the isosceles right triangle.
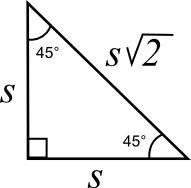
The sides of the isosceles right triangle also have a constant ratio s – s – s√ 2 . If the equal sides are each 4, then the hypotenuse will always be 4√ 2 .
The standardized tests for college entrance give answer choices with the √ 2 and do not ask you to solve √ 2 .
The 30-60-90 Right Triangle:
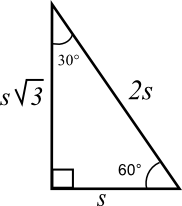
Standardized tests also love the 30-60-90 right triangle, (30-60-90 being the measures of each of the interior angles). These sides also have a constant ratio of s – s√ 3 – 2s
So, if you see a 30-60-90 right triangle with a hypotenuse of 8, then the shortest side must be half of 8 or 4. Then you will know that the other side is 4√ 3
The standardized tests for college entrance give answer choices with the √ 3 and do not ask you to solve √ 3 .

