Skip to content

Right-Angle Trig Flashcards

Back to “Basic Trigonometry” Page

You can increase your speed on the ACT by memorizing the four basic Pythagorean triples —

3-4-5 and multiples 6-8-10, 9-12-15, etc.
5-12-13 and multiples 10-24-26, 15-36-39, etc.
7-24-25 and multiples 14-48-50, 21-72-75, etc.
11-60-61 and multiples 22-120-122, etc.

—and by memorizing the basic trig functions in the word SOHCAHTOA.

sine (sin) = opposite/hypotenuse
cosine (cos) = adjacent/hypotenuse
tangent (tan) = opposite/adjacent

If you are lucky, you can also remember the reciprocals of the trig functions,

cosecant (csc) = 1/sin = hypotenuse/opposite
secant (sec) = 1/cos = hypotenuse/adjacent
cotangent (cot) = 1/tan = adjacent/opposite

Flashcard Practice

Standardized tests will often present diagrams of Pythagorean triples and omit the length of one of the sides. Use the diagrams and flashcards below to practice solving basic trig problems like those on standardized tests.

Use the 3-4-5 triangle above to answer the six flashcards below. The answers will be expressed in ratios (fractions).

  • sin θ
    4/5
  • cos θ
    3/5
  • tan θ
    4/3
  • csc θ
    5/4
  • sec θ
    5/3
  • cot θ
    3/4


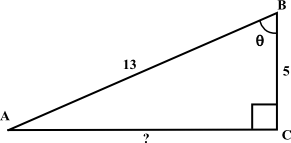
Use the diagram above to answer the four flashcards below.

  • sin θ
    12/13
  • cos θ
    5/13
  • tan of the angle at vertex A?
    5/12
  • cot of the angle at vertex A?
    12/5


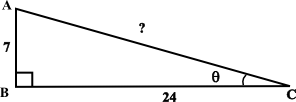
Use the diagram above to answer the four flashcards below.

  • sin θ
    7/25
  • cos θ
    24/25
  • csc of the angle at vertex A?
    25/24
  • sec of the angle at vertex A?
    25/7


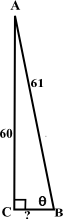
Use the diagram above to answer the four flashcards below.

  • tan θ
    60/11
  • cos θ
    11/61
  • cos of the angle at vertex A?
    60/61
  • sec of the angle at vertex A?
    61/60