Back to “Basic Trigonometry” Page
“Trigonometry” means “measuring triangles.” Basic trigonometry refers to the relationships between the measures of angles and sides of right triangles on a flat plane.

You have already seen some of these relationships in our old friend the 3-4-5 right triangle.
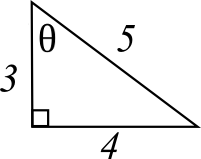
Notice the Greek letter theta θ in the upper angle of the diagram. It doesn’t mean anything in particular. Math people use it because it looks cool. It refers to a trigonometry function.
What is a Trig Function?
The acute angles of a right triangle can be expressed either in degrees or as a ratio of side lengths. For example, angle θ in the diagram above measures approximately 53°. But it can be expressed more precisely as a ratio of the opposite side to the hypotenuse or 4/5. This ratio is called the sine function. The three basic trig functions are sine, cosine, and tangent.
sine = opposite/hypotenuse
The sine of angle θ is the ratio of the opposite side over the hypotenuse, or 4 over 5.
cosine = adjacent/hypotenuse
The cosine of angle θ is the ratio of the adjacent side over the hypotenuse or 3/5.
tangent = opposite/adjacent
The tangent of angle θ is the ratio of the opposite side over the adjacent, or 4/3.
SOHCAHTOA
If you take the first letter of each of the bold-face words in the previous three sentences, you get the following word: sohcahtoa. This word can help you memorize the three basic trigonometry functions.
You will often find sine abbreviated to sin, cosine abbreviated to cos, and tangent abbreviated to tan.
Reciprocals of Trig Functions
“Reciprocal” is a fancy word for flipping a fraction. Since the basic trig functions are ratios (fractions), they can be flipped upside down to make their reciprocals.
| The reciprocal of sine is cosecant (csc): | csc = | 1/sin |
| The reciprocal of cosine is secant (sec): | sec = | 1/cos |
| The reciprocal of tangent is cotangent (cot): | cot = | 1/tan |

Consider the angle θ of the 3-4-5 triangle again.
If sin θ = 4/5, then csc θ = 5/4.
If cos θ = 3/5, then sec θ = 5/3.
If tan θ = 4/3, then cot θ = 3/4.

