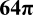The diagonal of a cube is nearly as simple as the Pythagorean theorem.
It is very simple:
(length)2 + (width)2 + (height)2 = (diagonal)2
In other words, you simply take the square root of the sum of the squares of the length, width, and height of the cube.
√(length)2 + (width)2 + (height)2 = d
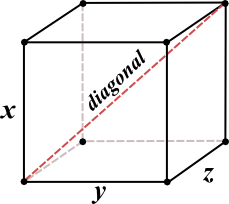
A simple equation for the diagram above would be this:
√x2 + y2 + z2 = d
Since the length, width, and height of a cube are equal, you can simply multiply one side squared by 3, like this:
√ 3(x2) = d
So, if a side of the cube above is equal to 1, then the equation for the diagonal is this:
√ 3(12) = d
√ 3 = d
It is handy to remember that √ 3 is approximately 1.7 or so. Just keep that tucked away in your memory.
And, if a side of the cube above is equal to 2, then the equation for the diagonal is this:
√ 3(22) = d
√ 3(4) = d
2√ 3 = d
And, if a side of the cube above is equal to 3, then the equation for the diagonal is this:
√ 3(32) = d
√ 3(9) = d
3√ 3 = d
You can now see a pattern developing. The diagonal of a cube is equal to any side of the cube times √ 3 .
See whether you can solve the flashcards below.
TAKE YOUR TIME!
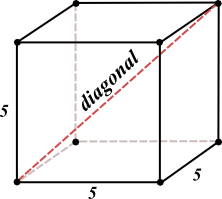
- What is the diagonal the cube above?
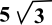
- What is the area of one face of the cube?52 or 25
- What is the surface area of the cube?6(25) or 150
- What is the volume of the cube?53 or 125
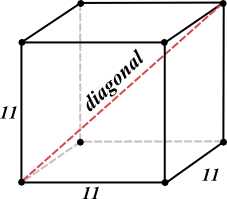
- What is the diagonal of the cube above?
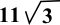
- What is the area of one face of the cube?112 or 121
- What is the surface area of the cube?6(121) or 726
- What is the volume of the cube?113 or 1,331
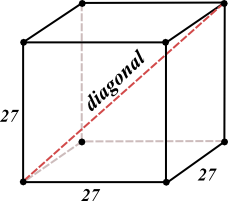
- What is the diagonal of the cube above?
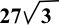
- What is the area of one face of the cube?272 or 729
- What is the surface area of the cube?6(729) or 4,374
- What is the volume of the cube?273 or 19,683
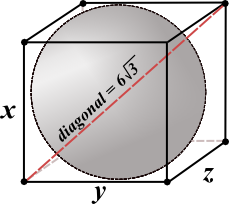
Assume that the sphere touches all six sides of the cube in the diagram above.
- What's the diameter of the sphere?6
- What is the area of one face of the cube?62 or 36
- What is the surface area of the cube?6(36) or 216
- What is the volume of the cube?63 or 216
WAIT! WAIT! Not done yet!
Recall the formula for volume of a sphere:
V = 4/3 π r3
And the formula for surface area of a sphere:
A = 4π r2
- What's the volume of the sphere?
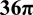
- What's the surface area of the sphere?
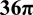

Now, try one more diagram. Remember that standardized tests often give answer choices with fractions, roots and π symbols in the answer.
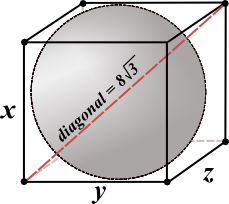
Assume that the sphere touches all six sides of the cube in the diagram above.
- What's the diameter of the sphere?8
- What is the area of one face of the cube?82 or 64
- What is the surface area of the cube?6(64) or 384
- What is the volume of the cube?83 or 512
- What's the volume of the sphere?
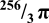
- What's the surface area of the sphere?