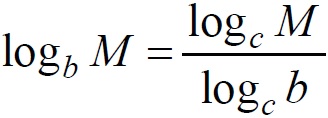Logarithms: Change of Base

Back to “Basic Algebra” Page

Sometimes a test or an assignment will tell you to solve something ridiculous like this:

17 = 5^x

And they want an actual approximate answer!

You might try to solve with this:

log₅ 17 = x

But unless you’ve spent 150 bucks on a fancy calculator that solves for log₅, you won’t get an answer. But you can use a 12-dollar Wal-Mart calculator to solve this, if you know the change of base formula.

Remember that the “log” button on your simple calculator is actually log₁₀. So, using the change of base formula for

log₅ 17 = x

You will get

Plugging that answer back into the original equation will give you

17 = 5^1.760374428 = 17.00000001

which is a very good approximation.

When there is no subscript number after “log” you can assume that it means log₁₀.

Use the flashcards below to practice the change of base formula.

• log₂ 3 =
  log 3 / log 2
• log₃ 7 =
  log 7 / log 3
• log₇ 11 =
  log 11 / log 7
• log₁₉ 23 =
  log 23 / log 19
• log₂₉ 31 =
  log 31 / log 29
• log₃₇ 41 =
  log 41 / log 37